A nuestro alrededor observamos continuamente simetrías, o su ruptura, en objetos tales como formas geométricas, materiales o sistemas biológicos. En Física estamos interesados en las simetrías de las leyes naturales, que históricamente han jugado un papel crucial en el avance del conocimiento. Es bien conocido que si las leyes dinámicas se mantienen invariantes al transformar las magnitudes físicas bajo cierta operación, esta invariancia puede indicar la existencia de observables conservados. Así, sabemos que la conservación del momento lineal está ligada a la invariancia bajo traslaciones espaciales, la del momento angular a las rotaciones, y la de la energía a las traslaciones temporales. Las transformaciones pueden ser en el espacio-tiempo, como las anteriores, pero también pueden ser transformaciones de grados de libertad internos, como las transformaciones gauge, que conducen a la conservación de la carga.

Si en el pasado las simetrías permitieron encontrar regularidades y orden en los fenómenos naturales cuando la dinámica de las fuerzas involucradas era aún desconocida, el último tercio del siglo XX ha conducido a una revolución conceptual por la que las propias interacciones aparecen como consecuencia de la imposición de simetrías locales, sea internas, en los casos de las interacciones electromagnéticas, débiles y fuertes, sea del espacio-tiempo, para la interacción gravitatoria. Este ingrediente ha sido esencial para la construcción del Modelo Estándar de la física de partículas, cuyo éxito experimental durante las últimas décadas ha sido espectacular.

Pero aún más importante que la existencia de una simetría es el posible mecanismo de su ruptura siguiendo un patrón definido. La contradicción aparente entre el acuerdo preciso del Modelo Estándar con los resultados experimentales y el hecho de que la simetría subyacente sólo es exacta para partículas de masa cero (cosa que, evidentemente, no es el caso para la mayoría de las partículas conocidas), necesita de un mecanismo de ruptura de la simetría muy sutil, capaz de generar las masas sin alterar la dinámica de las interacciones. El mecanismo de Brout-Englert-Higgs para encontrar soluciones físicas asimétricas a partir de una teoría simétrica resuelve el problema, dejando como señal medible la existencia del Bosón de Higgs, descubierto en el CERN, en los experimentos ATLAS y CMS del LHC, en 2012.

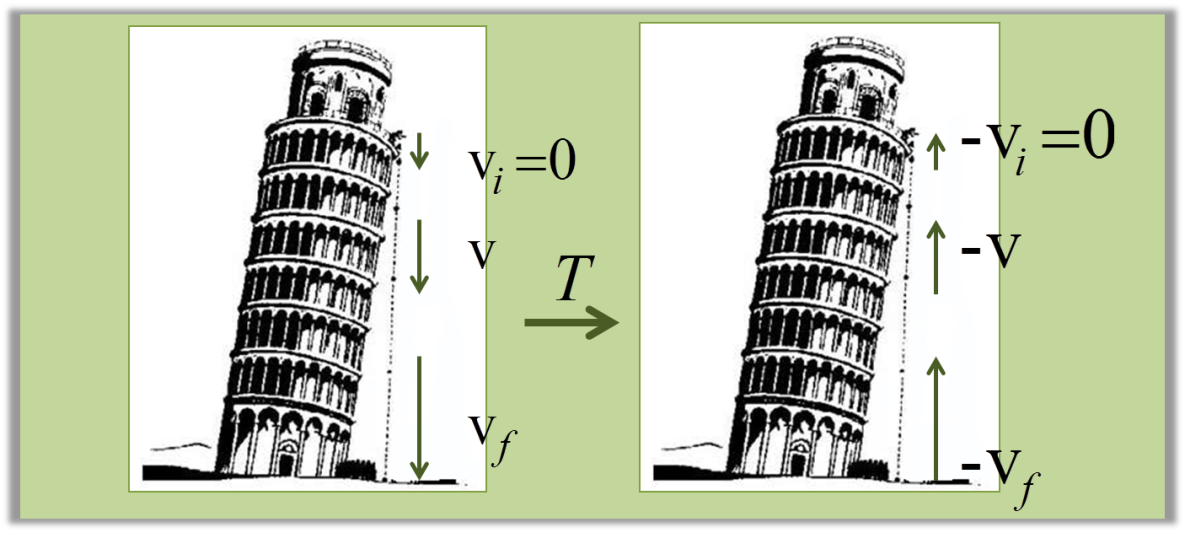
Las simetrías discretas en el espacio-tiempo, tales como paridad (o reflexión especular, simbolizada por P) e inversión temporal (T, representa la inversión de todos los movimientos, como vemos en la figura), así como la simetría interna de conjugación partícula-antipartícula (C), aparecen exactas en la naturaleza cuando las únicas interacciones en juego son las fuertes y electromagnéticas. Sin embargo, todas ellas sufren una ruptura ordenada para fenómenos en que intervienen las interacciones débiles, como por ejemplo la desintegración de algunas partículas y núcleos atómicos, y algunos procesos de fusión nuclear como los que ocurren en las estrellas, incluyendo nuestro Sol.

La violación de P fue descubierta en primer lugar en las desintegraciones beta de núcleos atómicos, y la de C y de P (por separado) en la desintegración del pión, en los años 50 del pasado siglo. La violación de CP fue descubierta inesperadamente en 1964 en la desintegración de kaones neutros, y se volvió a medir en las factorías de mesones B en 2001, mientras la demostración de la violación de T, usando el entrelazamiento de mesones B neutros, tuvo que esperar a 2012. En el Modelo Estándar se describen estas rupturas como consecuencia de dos facetas muy diferentes de la física: en el caso de P y C juega un papel fundamental la quiralidad, pues los campos levógiros y dextrógiros se transforman de forma distinta. Para CP y T es de suma importancia el contenido de partículas de la teoría, que necesita al menos tres familias de quarks y leptones para justificar la violación de esas simetrías.

Hasta el momento la única simetría discreta que permanece exacta es la combinación CPT. El Teorema CPT, demostrado durante los años 50 del siglo XX, establece que una teoría cuántica de campos que describa interacciones en un espacio-tiempo plano y que verifique estas tres condiciones: i) ser invariante Lorentz; ii) incluir sólo interacciones locales y iii) que su evolución sea unitaria, es necesariamente invariante bajo la transformación de simetría CPT. Los mejores límites actuales provienen de diferencias entre las masas de partículas y antipartículas, medida para los pares K⁰ – K̅⁰ (CPLEAR), B⁰ – B̅⁰ (BABAR) y p – p̅ (ASACUSA).

En teorías en las que alguna de esas condiciones no se cumpla rigurosamente, por ejemplo si la simetría Lorentz está violada o si las interacciones son no locales, puede darse la no invariancia bajo CPT. En los sistemas de mesones neutros este fenómeno se parametriza fenomenológicamente a través de una cantidad compleja, θ, que aparece en las matrices de masas. Otro mecanismo que puede producir la ruptura de CPT es que el propio operador CPT esté mal definido, como ocurre en algunas teorías de gravedad cuántica que predicen una estructura de “espuma” para el espacio-tiempo. En un reciente trabajo, investigadores del IFIC, en colaboración con colegas de King's College-London e IST-Lisboa, han encontrado que el tratamiento perturbativo de este último mecanismo conduce [1] a una modificación de las correlaciones cuánticas en el sistema de mesones neutros y añade una componente que debilita el entrelazamiento mediante una simetría de intercambio “equivocada”. Este efecto viene parametrizado por otra cantidad compleja, ω, que si es no nula da lugar a una señal experimental inequívoca [2]. En concreto, en los sistemas B⁰ – B̅⁰ debería observarse que las tasas de desintegración a los canales “sabor definido y después CP definido” y “CP definido y después sabor definido” (distinguidos por el orden temporal en que aparecen los estados finales) ya no estarían conectadas por la simetría de intercambio [3].

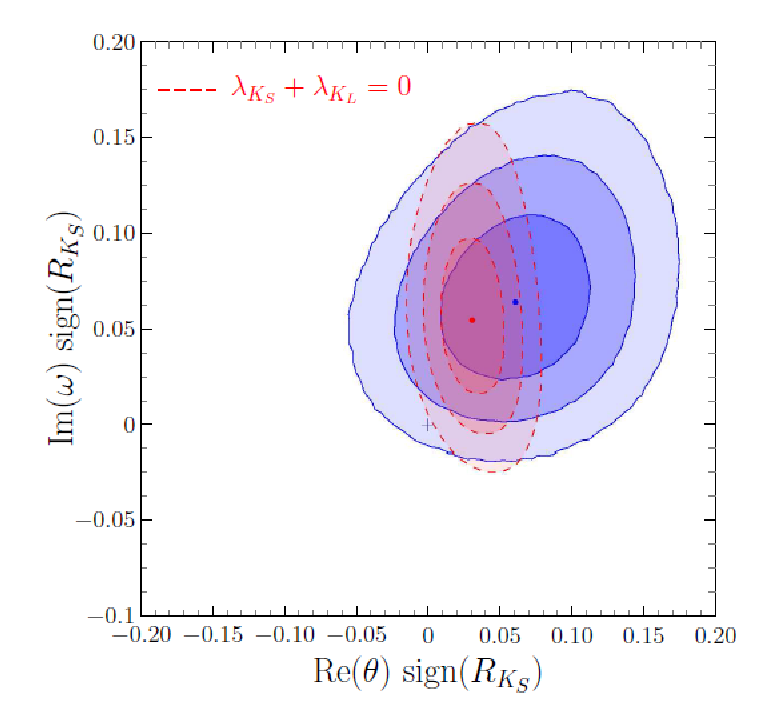El experimento BABAR ha medido las ocho tasas de desintegración relevantes para determinar el parámetro ω: las resultantes de combinar en el estado final los dos posibles sabores para el leptón ℓ^±, los dos posibles estados hadrónicos con CP definido, J/ψ K_S y J/ψ K_L, y las dos posibles ordenaciones temporales. El análisis de [2] ha encontrado un valor de Im(ω) que difiere de cero en unas 2σ. Además, este efecto es independiente de la posible violación de CPT debida a la parte real del parámetro θ, para la que el análisis también arroja un valor no nulo, de nuevo con unas 2σ de significación estadística. De hecho, si se repite el análisis asumiendo ω = 0 y considerando las asimetrías en T, CP y CPT por separado, el valor de θ obtenido no difiere del que se deduce en el caso anterior [3].

Los resultados finales para los dos tipos de ruptura de CPT se resumen en la figura, que muestra la parte imaginaria de ω respecto a la parte real de θ. Un enfoque conservador, dada la significación estadística de la medida actual, sugiere tomar estos valores de ω y θ como cotas superiores. En cualquier caso, la posibilidad de que alguno de ellos, o ambos, puedan ser no nulos, y por tanto la simetría CPT esté violada, añade un punto de expectación a los resultados que arrojarán en los próximos años BELLE‐II para mesones B y KLOE‐2 para mesones K. La ruptura de la simetría CPT conduciría a un cambio de paradigma en la física fundamental, sugiriendo que la teoría cuántica de campos como la hemos entendido hasta ahora debe ser reconsiderada.

[1] "Novel type of CPT violation for correlated EPR states", J. Bernabéu, N.E. Mavromatos, J. Papavassiliou. Phys.Rev.Lett. 92 (2004) 131601
[2] "The signal of ill-defined CPT weakening entanglement in the B_d system", J. Bernabéu, F.J. Botella, N.E. Mavromatos, M. Nebot. arXiv:1612.05652
[3] "Genuine T, CP, CPT asymmetry parameters for the entangled B_d system", J. Bernabéu, F.J. Botella, M. Nebot. JHEP 06 (2016) 100, arXiv:1605.03925