El año 2018 marca el centenario del nacimiento de uno de los físicos más prolíficos del siglo XX: Richard P. Feynman. Sus grandes aportaciones abarcan, además de la física de partículas, la física de la superfluidez del helio líquido superfrío. También fue pionero en introducir la nanotecnología y la computación cuántica como conceptos. Para conmemorar su vida y su legado científico, acaba de celebrase en Hungría un congreso financiado por la Acción COST PARTICLEFACE liderada por el IFIC, cuyo objetivo ha sido además el de presentar las técnicas más recientes en teoría cuántica de campos utilizadas para predecir el comportamiento de las partículas subatómicas en las colisiones a muy altas energías, como las que se producen en el LHC, a partir de los diagramas que llevan su nombre.

Richard Phillips Feynman nació en Nueva York el 11 de mayo de 1918, y recibió el Premio Nobel de Física en 1965, junto con Julian Schwinger y Shinichiro Tomonaga, por sus contribuciones al desarrollo de la Electrodinámica Cuántica (QED), la teoría cuántica de campos que describe las interacciones electromagnéticas. Feynman introdujo por primera vez los diagramas que llevan su nombre en una conferencia en las montañas Pocono de Pennsylvania durante la primavera 1948, precisamente para describir QED. La presentación de Feynman, sin embargo, no recibió, por su novedad, demasiada atención por parte de los asistentes. Por el contrario, en la misma conferencia, Schwinger ofreció una presentación de todo un día entero de duración sobre su versión de la teoría. Feynman y Schwinger no utilizaban el mismo lenguaje y les resultó muy difícil entenderse entre ellos, pese a ello llegaron a resultados similares lo cual sirvió para confirmar la validez de QED. La versión de Tomonaga llegaría poco después, y era algo más simple que la de Schwinger.

Feynman es también conocido por muchas otras aportaciones relevantes como el desarrollo completo del formalismo de integrales de camino en mecánica cuántica (basado en trabajos anteriores de P.A.M. Dirac), la física de la superfluidez del helio líquido superfrío, la cuantización de la gravedad y de las teorías de Yang-Mills, la forma V-A que describe las interacciones electrodébiles responsables de los procesos radioactivos, el modelo de partones, y por introducir de forma pionera la nanotecnología y la computación cuántica como conceptos. Es también muy conocido por su faceta publica, particularmente después de haber participado en la Comisión Rogers que investigó el accidente del transbordador espacial Challenger (1986), y por su labor pedagógica y divulgativa. Escribió además un par de libros semiautobiográficos muy conocidos (“Surely You're Joking, Mr. Feynman!” y “What Do You Care What Other People Think?”).

Diagramas de Feynman

Pero sin lugar a dudas los diagramas que llevan su nombre son su aportación más famosa ya que representan de forma gráfica y sencilla los procesos cuánticos que experimentan las partículas subatómicas cuando interaccionan entre ellas, y no sólo en QED sino también en cualquier teoría cuántica de campos. Estos diagramas están formados por una serie de vértices interconectados por líneas. Cada línea simboliza la propagación de una partícula de un punto del espacio-tiempo a otro, cada vértice la interacción entre varias partículas en un punto. Existen dos tipos de diagramas, aquellos en los que las líneas interconectadas forman circuitos cerrados, llamados loops, y aquellos en los que no, llamados diagramas de tipo árbol por su similitud con las ramas de un árbol.

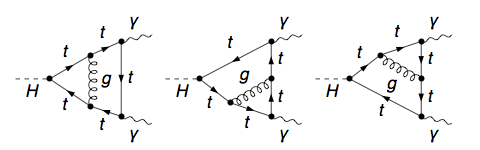
La ventaja principal de los diagramas de Feynman radica en la facilidad para trasladar los diagramas a expresiones matemáticas con las que los físicos pueden predecir cuál va a ser el comportamiento de las partículas subatómicas en procesos de colisión o desintegración a muy altas energías, por ejemplo, cuál es la probabilidad de producir un bosón de Higgs en el LHC, y cuál es la probabilidad de que ese bosón de Higgs se desintegre a dos fotones en lugar de hacerlo a dos quarks top. Cada teoría permite diferentes diagramas de Feynman y la translación de esos diagramas a fórmulas matemáticas depende también de la teoría. Así pues, los diagramas de Feynman son la forma más directa para obtener predicciones teóricas con las que comparar los datos experimentales y discernir qué teoría se ajusta mejor al experimento. Además, los diagramas de Feynman definen toda una serie de nuevas funciones matemáticas con propiedades muy interesantes. También desde el punto de vista matemático, los diagramas de Feynman introducen aspectos innovadores.

El campo teórico relacionado con las aplicaciones de los diagramas de Feynman ha experimentado un desarrollo espectacular en los últimos años motivado por las necesidades de disponer de predicciones teóricas de precisión y herramientas de análisis sofisticadas para analizar los datos del LHC. Cuando los físicos analizan un proceso de colisión en el LHC los diagramas de tipo árbol que lo describen representan únicamente una primera aproximación. Para mejorar la precisión de la teoría es necesario considerar también los diagramas de tipo loop, ya que son aquellos que incorporan las fluctuaciones cuánticas del vacío que contribuyen al mismo proceso. Cuanto mayor sea el número de loops que se incorporan a los cálculos teóricos mayor será la precisión de la teoría, pero también mayor el número de posibles fluctuaciones cuánticas y la complejidad de las expresiones matemáticas que se derivan de ellas. Cada nuevo loop introduce nuevas funciones matemáticas, y nuevos retos para los físicos teóricos.

A orillas del lago Balatón

Para celebrar el centenario este año del nacimiento de Richard P. Feynman, la Acción COST PARTICLEFACE liderada por el IFIC ha organizado recientemente una conferencia en Balatonfüred, a orillas del lago Balatón en Hungría, donde se presentaron y discutieron los últimos avances en el campo. La elección de Balatonfüred no ha sido casual y está justificada por varios motivos. En junio de 1972 tuvo lugar en Balatonfüred, organizada por el físico húngaro György Marx, la primera de una serie de conferencias internacionales sobre la física de neutrinos a la que asistieron 139 participantes entre ellos Richard P. Feynman, Tsung-Dao Lee (Nobel de Física 1957), tres investigadores que han recibido el premio Nobel posteriormente, y el hoy profesor de la Universidad de Zürich Zoltan Kunszt.

El lugar tiene también una historia interesante detrás. Desde 1926, Balatonfüred era frecuentado por el poeta, músico y artista indio Rabindranath Tagore. Tagore, primer no europeo que ganó el premio Nobel de Literatura en 1913, plantó un primer árbol en el lugar. A ese primer árbol acompañaron otros que fueron plantados por otros personajes indios en su visita a Tagore, dando lugar a lo que hoy se conoce como parque Tagore. Posteriormente, Salvatore Quasimodo (premio Nobel de Literatura 1959) plantó también un árbol, estableciendo así la tradición de que si algún premio Nobel visita Balatonfüred debe plantar un árbol. Este fue el caso de Feynman en 1972, a cuyo árbol acompañan hoy los árboles plantados entre otros por Bruno Pontecorvo, Nevill Francis Mott (Nobel de Física 1977), Eugene Wigner (Nobel de Física 1963) and Rudolf Mössbauer (Nobel de Física 1961), todos ellos identificados con su correspondiente placa conmemorativa.

Kunszt explicó cómo la conferencia de 1972 fue solo posible cuando más de 10 años después de la revolución de 1956, aplastada por la Unión Soviética, Hungría empezó a abrirse a la colaboración científica con el exterior, permitiendo a sus investigadores visitar otros países y organizar conferencias internacionales. Este es un claro ejemplo del valor diplomático de la Ciencia en general. Feynman, quien confirmó su asistencia a Balatonfüred en el último momento, impartió una charla sobre “What neutrinos can tell us about partons”. El modelo de partones había sido propuesto por Feynman en 1969 y describe los hadrones (e.g. protones y neutrones) como entes constituidos por partículas sub-subatómicas puntuales llamadas partones que a muy altas energías se comportan como si fuesen libres moviéndose en la dirección del hadrón del que forman parte. La conclusión de Feynman en Balatonfüred fue que los partones son quarks (hoy sabemos que son también gluones). Kunszt destacó que el modelo de partones no fue aceptado por la comunidad hasta la publicación en 1977 del artículo de Guido Altarelli y Giorgio Parisi “Asymptotic Freedom in Parton Language” que predice a partir de la teoría conocida como Cromodinámica Cuántica cuál es la densidad de esos partones dentro de los hadrones en función de la energía.

El profesor Kunszt hizo también hincapié en el artículo publicado en Acta Physica Polonica en 1963 que lleva por título “Quantum Theory of Gravitation”, y que está basado en las grabaciones en cinta de una conferencia impartida en Jablonna, Polonia. En este artículo de solo 14 páginas y 12 adicionales que reflejan la discusión posterior, Feynman introduce tres importantes conceptos novedosos: las conocidas como partículas fantasma de Fadeev-Popov (1967), el hoy llamado teorema del árbol de Feynman que establece una correspondencia entre diagramas de tipo loop y diagramas de tipo árbol con emisión de partículas adicionales, y las llamadas integrales de Berezin (1965) para fermiones, una extensión del formalismo de integrales de camino desarrollado por el propio Feynman.

En este artículo Feynman reconoce que accidentalmente y a propuesta de Murray Gell-Mann (Nobel en Física 1969) decidió aplicar el teorema del árbol a una teoría de Yang- Mills con masa nula por su analogía con la gravitación. Según Feynman, dicha teoría no puede existir puesto que produciría inmediatamente radiación fuera del núcleo. Aunque esta teoría no representaría un caso práctico, es más simple que la gravedad. Pues bien, dicha teoría se conoce actualmente como Cromodinámica Cuántica y describe con gran precisión las interacciones fuertes que ocurren a muy altas energías y que son las más relevantes en aceleradores hadrónicos como el LHC. Si la teoría funciona es porque hoy sabemos que la interacción fuerte se hace todavía más intensa a grandes distancias, no dejando escapar la radiación potencial del núcleo.

Muchos de los avances teóricos recientes en el campo están además indirectamente relacionados con el teorema del árbol Feynman. Este teorema ha servido también de inspiración para el teorema de dualidad loop-árbol y sus aplicaciones, propuesto y desarrollado por un grupo de investigadores del IFIC. La dualidad loop-árbol, como el teorema del árbol de Feynman, reduce el problema de muchos loops al cálculo de diagramas de tipo árbol, y presenta algunas ventajas interesantes respecto al teorema original de Feynman.

La conferencia concluyó con una vista al parque Tagore y sus árboles, entre ellos el árbol plantado por Feynman en 1972.

Referencias:

R.P. Feynman, “Quantum theory of gravitation”, Acta Phys. Polon. 24 (1963) 697-722

Neutrino '72: proceedings, Frenkel, A. & Marx, G. (Eds.), Published by Omkdk-Technoinform, Hungary (1972)

“Selected papers of Richard Feynman: With commentary”, L.M. Brown (Ed.) World Scientific Series in 20th Century Physics – Vol. 27 (2000)

S. Catani, T. Gleisberg, F. Krauss, G. Rodrigo and J.C. Winter, “From loops to trees by-passing Feynman's Theorem”, JHEP 0809 (2008) 065 [arXiv:0804.3170 hep-ph].

Acción COST CA16201 PARTICLEFACE. https://particleface.eu