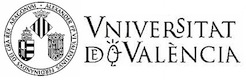La Cromodinámica Cuántica (Quantum Chromodynamics, QCD, en inglés) es la teoría de las interacciones fuertes que mantienen unidos los quarks dentro de los protones y neutrones, los constituyentes de la materia ordinaria. Igual que la electrodinámica cuántica (QED, en inglés), es una teoría gauge, donde la fuerza entre partículas cargadas proviene del intercambio de bosones vectoriales intermediarios de masa nula: un fotón en el caso de QED y ocho gluones en el caso de QCD. La simetría gauge de QCD está basada en el grupo unitario especial, SU(3), y la carga asociada se denomina color. Los quarks poseen tres cargas básicas o colores: rojo, azul y verde.

QCD es extremadamente predictiva. Una constante de acoplamiento, seis masas de quarks y el llamado ángulo theta del vacío son los únicos parámetros libres a partir de los cuales una plétora de fenómenos pueden ser en principio predichos, tales como el espectro de los hadrones y sus interacciones. El famoso ángulo theta del vacío es la única fuente de violación de CP (asimetría entre materia y antimateria) de las interacciones fuertes, pero su valor antinaturalmente pequeño ha sido acotado por la medida del momento dipolar eléctrico del neutrón. El hecho de que este parámetro sea tan pequeño constituye el llamado problema de CP fuerte.

A pesar de la simplicidad del lagrangiano de QCD, sus predicciones cuantitativas son no triviales. Efectivamente, los quarks o gluones coloreados no han sido observados de manera aislada. Este hecho se conoce como confinamiento, una propiedad esencial de QCD que implica que sólo los estados que no poseen carga de color pueden propagarse libremente. Los compuestos neutros que observamos en la naturaleza son los hadrones: mesones compuestos de un quark y un antiquark, o bariones compuestos de tres quarks.

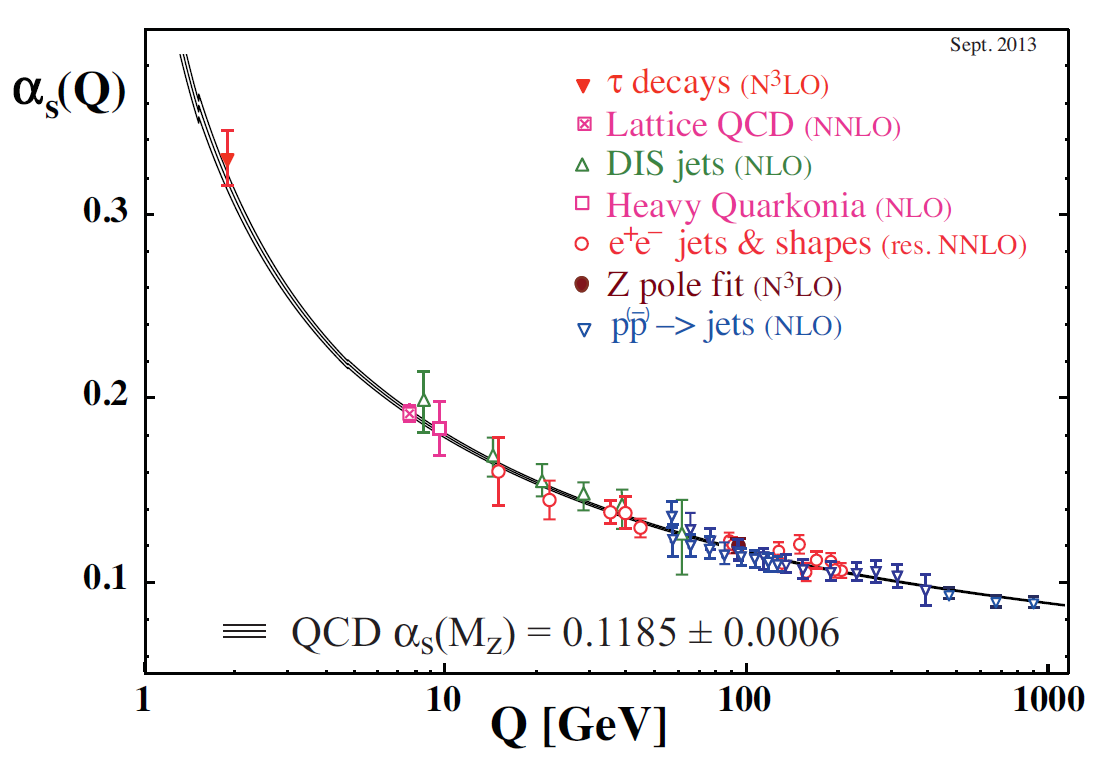
Se cree que el origen del confinamiento radica en la propiedad de la libertad asintótica, descubierta por Gross, Wilczek y Politzer (vencedores del premio Nobel en 2004), que consiste en el hecho que la intensidad de la interacción de QCD decrece a cortas distancias (o altas energías) y aumenta a grandes distancias (o bajas energías). Este comportamiento ha sido observado experimentalmente, como se muestra en la figura de la derecha. Puesto que el acoplamiento fuerte es débil a altas energías, se puede usar la teoría de perturbaciones de forma fiable en este régimen y explica perfectamente la evolución de la constante de acoplamiento. Por otra parte, a bajas energías, el desarrollo perturbativo se rompe, y el confinamiento entra en escena.

¿ Es QCD una teoría confinante ? Esta es una de las cuestiones fundamentales y constituye uno de los famosos problemas del Milenio. Lattice QCD (LQCD) fue inventada por K. Wilson (premio Nobel en 1982) hace más de 40 años para comprender la libertad asintótica y la propiedad confinante de QCD a partir de primeros principios.

La idea clave es substituir el continuo espacio-tiempo cuadridimensional infinito por un retículo hipercúbico finito. Los campos de quark se definen en los nodos de la red mientras que los campos de gluón viven en los eslabones y la teoría de campos cuánticos se hace corresponder con un sistema estadístico clásico. En efecto, Wilson tomó prestado de la mecánica estadística el desarrollo en una constante de acoplamiento fuerte (equivalente a una expansión para temperatura alta) para demostrar el confinamiento al orden más bajo en 1/g². Desgraciadamente esta demostración no es definitiva, porque en esta aproximación la teoría no tiene un límite al continuo. La existencia de un límite al continuo puede en cambio ser demostrada en el régimen opuesto de acoplamiento débil. No obstante, la construcción de Wilson hizo de QCD una teoría tratable mediante métodos numéricos. En efecto, una consecuencia muy importante de la discretización es que la medida de las integrales funcionales son productos de un gran pero contable número de diferenciales. Debido a que el número de grados de libertad es muy grande, son imprescindibles los métodos de Monte Carlo y grandes ordenadores masivamente paralelos. La mayoria de los resultados cuantitativos de la moderna LQCD están basados en estudios numéricos de este tipo.

Una de las aplicaciones más consolidadas de las simulaciones de LQCD es precisamente el estudio del confinamiento y de la libertad asintótica. Las simulaciones han demostrado que la energía entre un par de quark y antiquark aumenta linealmente con su separación. La evolución de la constante de acoplamiento gauge de QCD también ha sido estudiada más allá de la teoría de perturbaciones confirmando la propiedad de libertad asintótica y proporcionando la determinación más precisa de la intensidad del acoplamiento de QCD, como puede verse en la figura arriba a la derecha.

Sin embargo, aún existen importantes limitaciones en las simulaciones en la red. Una de las mayores dificultades tiene que ver con el tratamiento de los grados de libertad de los quarks. Es muy dificil mantener las propiedades quirales de la acción en el continuo, lo que es imprescindible para simular los quarks ligeros. En la última década se han realizado progresos muy importantes en este problema. Se han descubierto discretizaciones fermiónicas que preservan las propiedades quirales (domain wall fermions y overlap fermions), y variantes de los fermiones Wilson computacionalmente más eficientes con un comportamiento quiral mejorado, los llamados twisted-mass Wilson fermions, han conseguido que las simulaciones del régimen quiral sean factibles. Más aún, importantes mejoras algorítmicas (como Schwarz preconditioning, deflation acceleration, trivializing maps y el Wilson flow y open boundary conditions y twisted-mass reweighting) han sido necesarias para incorporar eficientemente la contribución de los quarks a la integral de camino, que representa los efectos cuánticos de pares virtuales quark-antiquark. El estado actual de la técnica de las simulaciones incluye los efectos más relevantes de los quarks: aquellos de los dos quarks más ligeros, el u y el d (simulaciones Nf=2), estos últimos más el quark extraño (simulaciones Nf=2+1) y más recientemente también el quark encantado (simulaciones Nf=2+1+1) ha sido incluido.

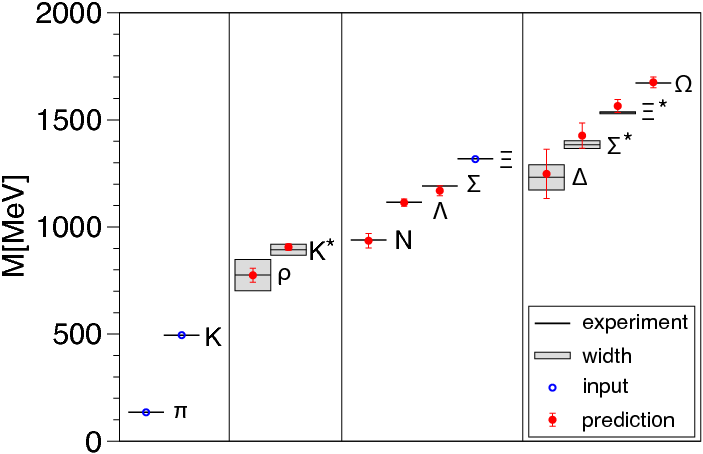
El método de las simulaciones en la red no es universalmente aplicable pero se ha utilizado para calcular muchas cantidades físicas de manera no perturbativa a partir de primeros principios, incluyendo el espectro de masas hadrónico, el condensado de quarks, las masas de los quarks, las constantes de desintegración y los factores de forma de las desintegraciones leptónicas y semileptónicas. Además, el enfoque de la red es obligado en el cálculo de los elementos de matriz débiles, tales como los parámetros B de las oscilaciones de mesón y antimesón que son muy importantes para la determinación precisa de los elementos de la matriz CKM de mezcla, y para realizar chequeos de consistencia de unitariedad y búsquedas de posible física más allá del Modelo Estándar. Otra importante contribución de QCD en la red es el cálculo de los momentos de las funciones de distribución partónicas y gluónicas, esenciales para la determinación de secciones eficaces en el LHC y Tevatron, además de los términos sigma isosinglete y extraño que juegan un papel en las búsquedas directas de materia oscura. Las simulaciones en la red es también el método para estudiar QCD en condiciones extremas (alta temperatura y densidad) tales como las que había en el Universo primordial o en objectos astrofísicos como las estrellas de neutrones.

“Probing the chiral regime of Nf= 2 QCD with mixed actions”, F. Bernardoni, P. Hernandez, N. Garron, S. Necco, C. Pena. Phys.Rev. D83 (2011) 054503

“On K ---> pi pi amplitudes with a light charm quark”, L. Giusti, P. Hernandez, M. Laine, C. Pena, J. Wennekers, H. Wittig. Phys.Rev.Lett. 98 (2007) 082003

“Up, down, strange and charm quark masses with N_f =2+1+1 twisted mass lattice QCD”, ETM Collaboration, N. Carrasco et al. Nucl. Phys. B887 (2014) 19-68

“B-physics from N_f =2 tmQCD: the Standard Model and beyond”, ETM Collaboration, N. Carrasco et al. JHEP 1403 (2014) 016

“Kaon mixing beyond the SM from N_f =2 tmQCD and model independent constraints from the UTA”, ETM Collaboration, V. Bertone et al. JHEP 1303 (2013) 089

“Light hadrons from Lattice QCD with light (u,d), strange and charm dynamical quarks”, ETM Collaboration, R. Baron et al. JHEP 1006 (2010) 111