Lattice QCD, the numerical approach to the strong force
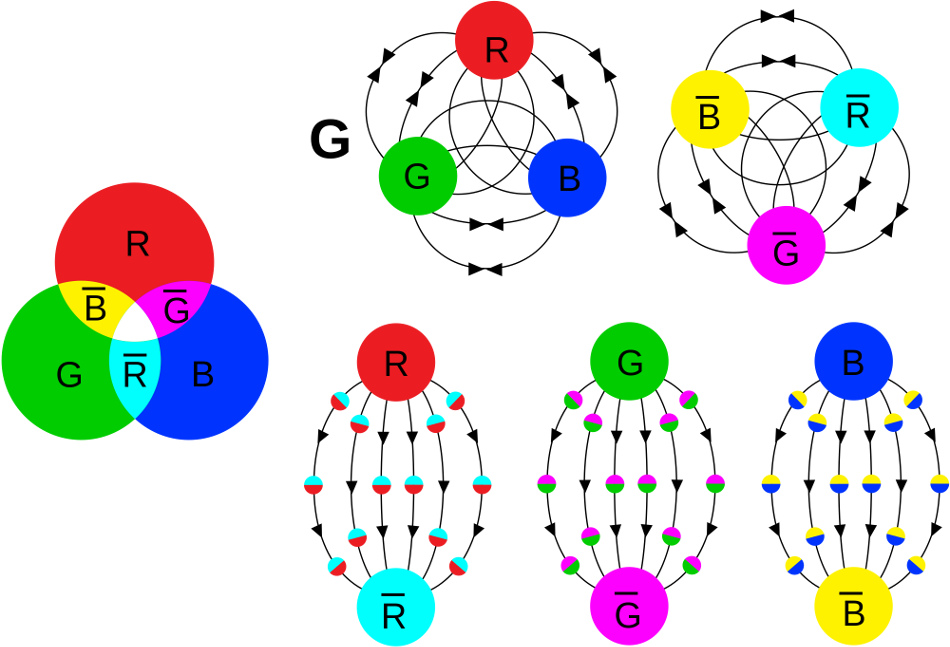
Quantum Chromodynamics (QCD) is the theory of the strong interactions that glue together quarks inside protons and neutrons, the constituents of ordinary matter. Like electromagnetism (QED), it is a gauge theory, where the force between charged particles originates in the exchange of intermediate massless vector bosons: one photon in the case of QED and eight gluons in the case of QCD. The gauge symmetry of QCD is based on the special unitary group, SU(3), and the associated charge is called color. Quarks carry three basic charges or colors: red, blue and green.
QCD is extremely predictive. One gauge coupling constant, six quark masses and the so-called theta vacuum angle are the only free parameters from which a plethora of phenomena can in principle be predicted, such as the spectrum of hadrons and their interactions. The famous theta vacuum angle is the only source of CP violation (asymmetry between matter and antimatter) of the strong interactions, but has been constrained from the measurement of the neutron electric dipole moment to be unnaturally small. The fact that this parameter is so small is the so-called strong CP problem.
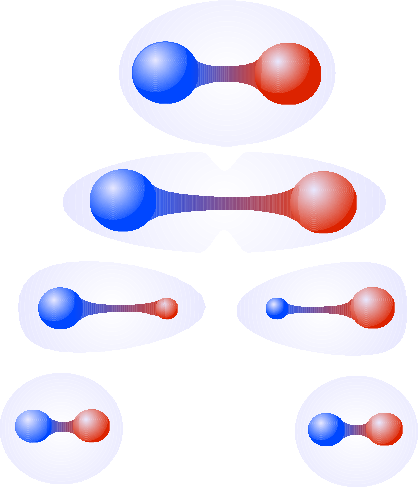
In spite of the simplicity of the QCD Lagrangian, quantitative predictions are highly non trivial. Indeed the colored quarks or gluons have not been observed in isolation. This fact is referred to as confinement, an essential property of QCD which implies that only states that carry no color charge can propagate freely. The neutral composites that we observe in nature are the hadrons: mesons composed of a quark and an antiquark, or baryons composed of three quarks.
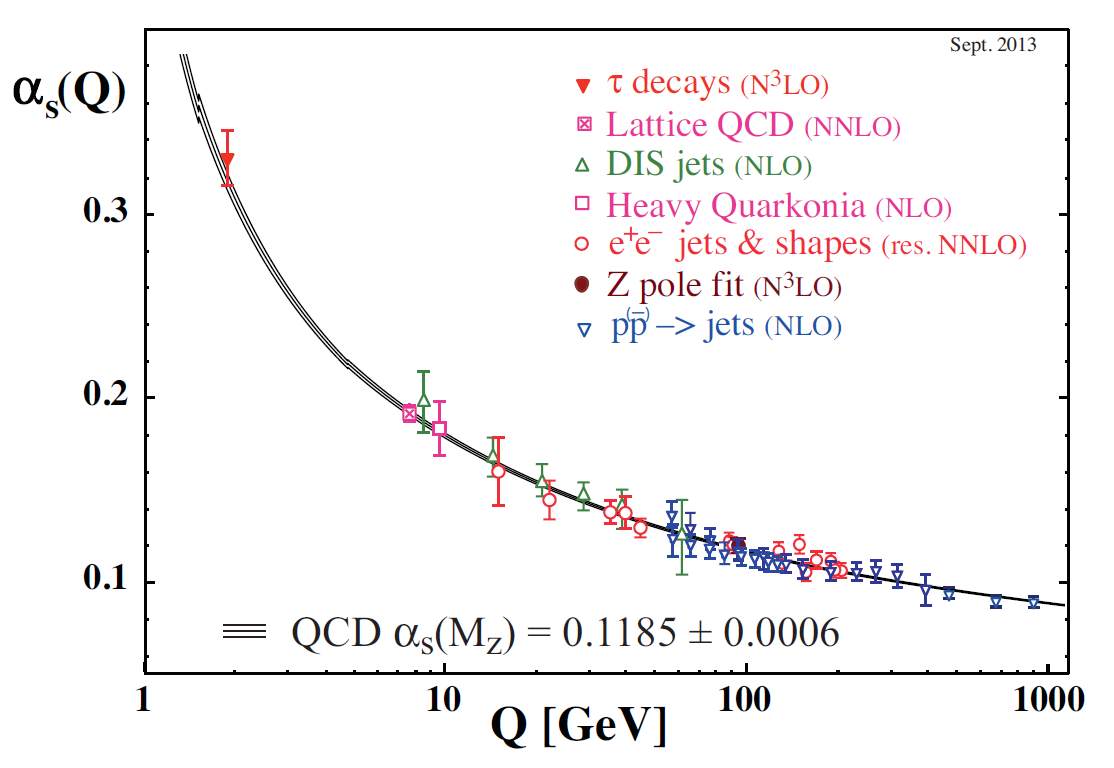
It is believed that the origin of confinement lies in the property of asymptotic freedom, discovered by Gross, Wilczek and Politzer (Nobel Prize winners in 2004), which refers to the fact that the strength of the QCD interaction decreases at short distances (or high energies) and increases at long distances (or low energies). This behaviour has been observed experimentally, as shown in the figure on the right. Since the strong coupling is weak at high energies, perturbation theory can be reliably used in this regime and nicely explains the running of the coupling. On the other hand, at low energies, the perturbative expansion breaks down, and confinement sets in.
Is QCD a confining theory ? This is one of the fundamental questions and constitutes one of the famous Millennium Prize problems. Lattice QCD (LQCD) was invented by K. Wilson (Nobel prize in 1982) more than 40 years ago to understand asymptotic freedom and the confining property of QCD from first principles.
The key idea is to replace the infinite four-dimensional space-time continuum with a finite hypercubic lattice. Quark fields are defined at the lattice points whereas gluon fields live on the links and the quantum field theory is mapped into a classical statistical system. In fact, Wilson borrowed the strong-coupling expansion from statistical mechanics (equivalent to a high temperature expansion) to demonstrate confinement to lowest order in 1/g2. Unfortunately this proof is not definite, because in this approximation the theory does not have a continuum limit. The existence of a continuum limit can instead be proven in the opposite weak coupling regime. Nevertheless Wilson's construction made QCD tractable by numerical methods. Indeed a very important consequence of the discretization is that the measure of the functional integrals are products of a large but countable number of differentials. Since the number of degrees of freedom is very large, Monte Carlo methods and big massively parallel computers are mandatory. Most of the quantitative results of modern LQCD are based on such numerical studies.
One of the more mature applications of LQCD simulations is precisely the study of confinement and asymptotic freedom. Simulations have demonstrated that the energy between a quark and antiquark pair increases linearly with their separation. The running of the QCD gauge coupling has been also studied beyond perturbation theory confirming the property of asymptotic freedom and providing the most accurate determination of the QCD coupling strength, as can be seen from the upper-right figure.
Nevertheless, there are still important limitations in lattice simulations. One of the major difficulties has to do with the treatment of the quark degrees of freedom. It is very difficult to maintain the chiral properties of the continuum action, which is mandatory to simulate the light quarks. Very important progress has been made in the last decade on this problem. Fermion discretizations that can maintain chiral properties have been found (domain wall fermions and overlap fermions), and variants of the most cost-effective Wilson fermions with improved chiral behaviour, the so-called twisted-mass Wilson fermions, have made the simulation of the chiral regime feasible. Furthermore important algorithmic improvements (like Schwarz preconditioning, deflation acceleration, trivializing maps and the Wilson flow and open boundary conditions and twisted-mass reweighting) have been necessary to incorporate efficiently the contribution of quarks to the path integral, which represents the quantum effects of virtual quark-antiquark pairs. State-of-the-art simulations nowadays include the most relevant quark effects: those of the two lightest u and d quarks (Nf=2 simulations), those plus the strange quark (Nf=2+1 simulations) and more recently also the charm quark (Nf=2+1+1 simulations) has been included.
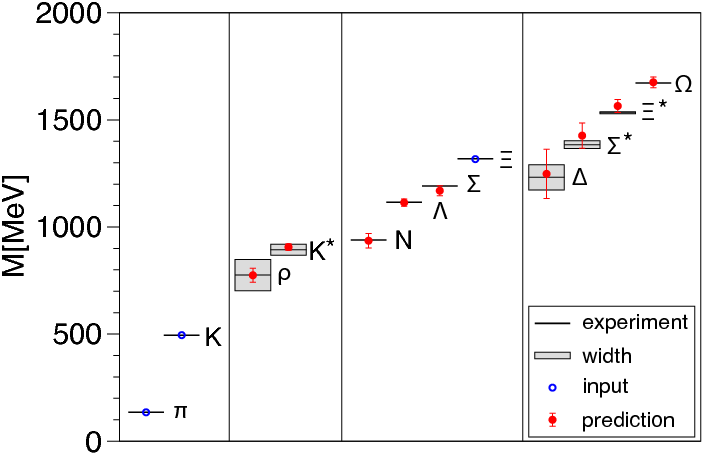
The lattice approach is not universally applicable but has been used to compute from first principles many physical quantities beyond the QCD coupling constant, including the hadron mass spectrum, the quark condensate, quark masses, decay constants and form factors for leptonic and semileptonic decays. Also the lattice approach is mandatory in computing weak matrix elements, such as the K or B-parameters of meson-antimeson oscillations that are very important for the precise determination of the elements of the CKM mixing matrix, and for performing consistency checks of unitarity and searching possible physics beyond the SM. Another important contribution of lattice QCD is the computation of the moments of parton and gluon distribution functions, essential for the calculation of cross sections in the LHC and Tevatron, as well as the isosinglet and strange sigma terms that play a role in the direct searches for dark matter. The lattice is also the method to study QCD in extreme conditions (high temperature and density) such as those that would be found in the early Universe or in astrophysical objects such as neutron stars.
“Probing the chiral regime of Nf= 2 QCD with mixed actions”, F. Bernardoni, P. Hernandez, N. Garron, S. Necco, C. Pena. Phys.Rev. D83 (2011) 054503
“On K ---> pi pi amplitudes with a light charm quark”, L. Giusti, P. Hernandez, M. Laine, C. Pena, J. Wennekers, H. Wittig. Phys.Rev.Lett. 98 (2007) 082003
“Up, down, strange and charm quark masses with Nf =2+1+1 twisted mass lattice QCD”, ETM Collaboration, N. Carrasco et al. Nucl. Phys. B887 (2014) 19-68
“B-physics from Nf =2 tmQCD: the Standard Model and beyond”, ETM Collaboration, N. Carrasco et al. JHEP 1403 (2014) 016
“Kaon mixing beyond the SM from Nf =2 tmQCD and model independent constraints from the UTA”, ETM Collaboration, V. Bertone et al. JHEP 1303 (2013) 089
“Light hadrons from Lattice QCD with light (u,d), strange and charm dynamical quarks”, ETM Collaboration, R. Baron et al. JHEP 1006 (2010) 111